When we say no allocation in openLCA, it means "pull in the processes into the technology matrix A and intervention matrix B according their product demand without applying any allocation factors".
Here is a small example: suppose we have a process `p1` that has an output of 0.5 units of product `p11`, 1.5 units of product `p12`, and 2.0 units of emission `e1`. Then there are two processes `p2` and `p3` that consume one unit of `p11` and `p12` respectively. Finally, there is a process `p4` that consumes one unit of `p2` and `p3`. Here is the product system graph of that example:
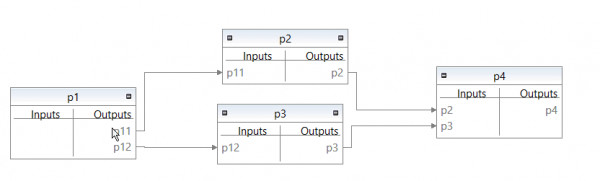
and the model in a tiny syntax (`->` means output, `<-` means input):
p1 -> 0.5 p11
p1 -> 1.5 p12
p1 -> 2.0 e1
p2 <- 1.0 p11
p3 <- 1.0 p12
p4 <- 1.0 p2
p4 <- 1.0 p3
For the example the technology matrix then looks like this:
# p11 p12 p2 p3 p4
A = [ 0.5 0.0 -1.0 0.0 0.0 ; # p11
0.0 1.5 0.0 -1.0 0.0 ; # p12
0.0 0.0 1.0 0.0 -1.0 ; # p2
0.0 0.0 0.0 1.0 -1.0 ; # p3
0.0 0.0 0.0 0.0 1.0 ] # p4
The intervention matrix B then looks like this when allocation is set to `none` (no allocation factor is applied for `p11` and `p12`):
# p11 p12 p2 p3 p4
B = [ 2.0 2.0 0.0 0.0 0.0]
Now, when we want to calculate the system for one unit of `p4`, so we have a demand vector:
d = [ 0.0 ; # p11
0.0 ; # p12
0.0 ; # p2
0.0 ; # p3
1.0 ] # p4
we get the result `g = B * (A \ d)` of `5.333` units of `e1` (note that openLCA also reports the unlinked product amounts in this case).
When we apply allocation factors in process `p1` based on the product amounts we get a factor of `0.25` for `pp1` and 0.75 for product pp2. In the example above, only the intervention matrix changes:
# p11 p12 p2 p3 p4
B = [ 0.5 1.5 0.0 0.0 0.0]
... and we get the result of 2.0 units of `e1`.