The use of cut-off reduces the required memory of openLCA and the calculation time. Unfortunately, (and not surprisingly) this goes along with a loss of detail in the results. Let's assume a linear chain of four processes with only one input and output respectively. Each process has an output and demands a specific input from the previous process.
The cut-off depends on a scaling factor which is the ratio of demand of the specific process and the output of the previous process multiplied by the scaling factor of the specific process (the scaling factor of the first process is always 1). In this way, the scaling factor is continued and shrinks with the outline level of a product system.
e.g. Scaling factor of process 3 = Demand of process 3 / Output of process 3 * Scaling factor of process 2

Whenever the cut-off is higher than the scaling factor, the process chain is cut off at the specific link.
It should be noted that the given example is simplified. Actual LCA models are likely to have more than one input/output per process as well as non-linear process chains and multiple linkages per process.
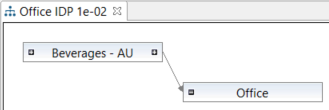
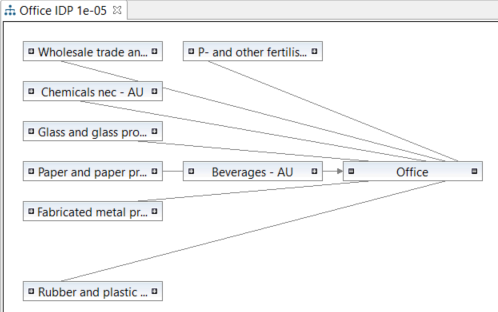
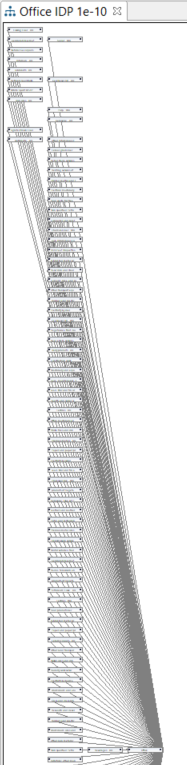
This is an example of how cut-off may affect the complexity of one and the same product system and its model graph in openLCA 1.7
Cut-off: 1e-02
Cut-off: 1e-03

Cut-off: 1e-05
Cut-off: 1e-10
Learn about provider linking in the following answer: https://ask.openlca.org/585/what-provider-linking-when-creatinging-new-product-system?show=627#a627
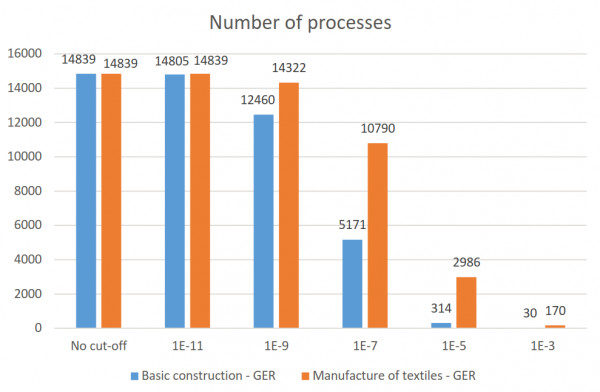
A very nice overview of how cut-off affects the size of your product system is given in the documentation of the PSILCA database: https://nexus.openlca.org/database/PSILCA (‘Documents’ tab). Section '4.3 Variation of results due to different cut-off criteria':
Number of processes depending on different cut-off criteria for two product systems: